TRAX, a Tweakable Block Cipher
Trax-L-17 (pronounced “T-rax”) is a tweakable block cipher operating on a large 256-bit block. It applies a 256-bit key and 128-bit tweak. To the best of our knowledge, the only
other large tweakable block cipher is Threefish which was used as a building for
the SHA-3 candidate Skein. Unlike this cipher, Trax-L-17 uses 32-bit words that
are better suited for vectorized implementation as well as on micro-controllers.
Another improvement of Trax-L-17 over Threefish is the fact that we provide strong bounds for the probability of all linear trails and all (related-tweak) differential trails. Because of its Substitution-Permutation Network structure, Trax is indeed inherently easier to analyze. Such a large tweakable block cipher can provide robust authenticated encryption, meaning that it can retain a high security level even in case of nonce misuse or in the presence of quantum adversaries, as argued in Saturnin specification. The performance penalty of such guarantees can be minimized using vectorization and/or parallelism.
A tweakable block cipher lends itself well to a parallelizable mode of operation
such as ΘCB, a variant of OCB which saves its complex overhead needed to
turn a regular block cipher into a tweakable one. Since our block size is equal to
256 bits, attacks relying on collisions obtained via the birthday paradox are non-
issue with Trax-L-17. Some modes such as the Synthetic Counter-in-Tweak
can retain a security level up to the birthday bound in case of nonce misuse. As
suggested in Saturnin specification, using a 256-bit block cipher can also help providing post-
quantum security in cases where the attacker is given a lot of power (e.g. if the
primitive runs on a quantum computer).
Description
The following figure captures the high-level structure of one step in Trax-L. Here, \(A_c\) denotes the ARX-box Alzette with the constant \(c\); \(\ell'\) is a linear bijection of \((\mathbb{F}_2^{16})^4\) defined as
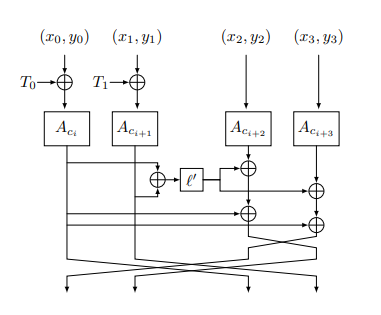
Below, we provide a reference implementation of Trax-L-17 in C.
#define ROT(x, n) (((x) >> (n)) | ((x) << (32-(n))))
#define ALZETTE(x, y, c) \
(x) += ROT((y), 31), (y) ^= ROT((x), 24), \
(x) ^= (c), \
(x) += ROT((y), 17), (y) ^= ROT((x), 17), \
(x) ^= (c), \
(x) += (y), (y) ^= ROT((x), 31), \
(x) ^= (c), \
(x) += ROT((y), 24), (y) ^= ROT((x), 16), \
(x) ^= (c)
#define ALZETTE_INV(x, y, c) \
(x) ^= (c), \
(y) ^= ROT((x), 16), (x) -= ROT((y), 24), \
(x) ^= (c), \
(y) ^= ROT((x), 31), (x) -= (y), \
(x) ^= (c), \
(y) ^= ROT((x), 17), (x) -= ROT((y), 17), \
(x) ^= (c), \
(y) ^= ROT((x), 24), (x) -= ROT((y), 31)
#define NSTEPS 17
#define ELL(x) (ROT(((x) ^ ((x) << 16)), 16))
static const uint32_t RCON[8] = { \
0xB7E15162, 0xBF715880, 0x38B4DA56, 0x324E7738, \
0xBB1185EB, 0x4F7C7B57, 0xCFBFA1C8, 0xC2B3293D };
void traxl17_genkeys_ref(uint32_t *subkeys, const uint32_t *key)
{
uint32_t key_[8], tmp;
int b, s; // branch and step counter
memcpy(key_, key, 32);
for (s = 0; s < NSTEPS+1; s++) {
// assign 8 sub-keys
for (b = 0; b < 8; b++)
subkeys[8*s+b] = key_[b];
// update master-key
key_[0] += key_[1] + RCON[(2*s)%8];
key_[2] ^= key_[3] ^ s;
key_[4] += key_[5] + RCON[(2*s+1)%8];
key_[6] ^= key_[7] ^ ((uint32_t) (s << 16));
// rotate master-key
tmp = key_[0];
for (b = 1; b < 8; b++)
key_[b-1] = key_[b];
key_[7] = tmp;
}
}
void traxl17_enc_ref(uint32_t *x, uint32_t *y, const uint32_t *subkeys,
const uint32_t *tweak)
{
uint32_t tmpx, tmpy;
int b, s; // branch and step counter
for (s = 0; s < NSTEPS; s++) {
// add tweak to state if step-counter is odd
if ((s % 2) == 1) {
x[0] ^= tweak[0]; y[0] ^= tweak[1];
x[1] ^= tweak[2]; y[1] ^= tweak[3];
}
// add subkeys to state and execute ALZETTEs
for (b = 0; b < 4; b++) {
x[b] ^= subkeys[8*s+2*b];
y[b] ^= subkeys[8*s+2*b+1];
ALZETTE(x[b], y[b], RCON[(4*s+b)%8]);
}
// linear layer (see Sparkle256 permutation)
tmpx = ELL(x[2] ^ x[3]); y[0] ^= tmpx; y[1] ^= tmpx;
tmpy = ELL(y[2] ^ y[3]); x[0] ^= tmpy; x[1] ^= tmpy;
tmpx = x[0]; x[0] = x[3]; x[3] = x[1]; x[1] = x[2]; x[2] = tmpx;
tmpy = y[0]; y[0] = y[3]; y[3] = y[1]; y[1] = y[2]; y[2] = tmpy;
}
// add subkeys to state for final key addition
for (b = 0; b < 4; b++) {
x[b] ^= subkeys[8*NSTEPS+2*b];
y[b] ^= subkeys[8*NSTEPS+2*b+1];
}
}
void traxl17_dec_ref(uint32_t *x, uint32_t *y, const uint32_t *subkeys,
const uint32_t *tweak)
{
uint32_t tmpx, tmpy;
int b, s; // branch and step counter
// add subkeys to state for initial key addition
for (b = 0; b < 4; b++) {
y[b] ^= subkeys[8*NSTEPS+2*b+1];
x[b] ^= subkeys[8*NSTEPS+2*b];
}
for (s = NSTEPS-1; s >= 0; s--) {
// inverse linear layer (see Sparkle256 permutation)
tmpy = y[0]; y[0] = y[2]; y[2] = y[1]; y[1] = y[3]; y[3] = tmpy;
tmpx = x[0]; x[0] = x[2]; x[2] = x[1]; x[1] = x[3]; x[3] = tmpx;
tmpy = ELL(y[2] ^ y[3]); x[0] ^= tmpy; x[1] ^= tmpy;
tmpx = ELL(x[2] ^ x[3]); y[0] ^= tmpx; y[1] ^= tmpx;
// add subkeys to state and execute inverse ALZETTEs
for (b = 0; b < 4; b++) {
ALZETTE_INV(x[b], y[b], RCON[(4*s+b)%8]);
y[b] ^= subkeys[8*s+2*b+1];
x[b] ^= subkeys[8*s+2*b];
}
// add tweak to state if step-counter is odd
if ((s % 2) == 1) {
y[1] ^= tweak[3]; x[1] ^= tweak[2];
y[0] ^= tweak[1]; x[0] ^= tweak[0];
}
}
}
Performance
In summary, Trax-L-17 can be used in SCT mode to provide 128 bits of
security in case of nonce-misuse, and its large block size can frustrate some
quantum attacks when used in the same mode as Saturnin: it can be used to
offer a very robust authenticated encryption. On a Cortex-M3 microcontroller,
the generation of subkeys, encryption, and decryption has an execution time
of 925, 2435, and 2464 clock cycles, respectively. These results are based on a
standard C implementation, whereby we determined the execution times with
help of the cycle-accurate instruction set simulator of Keil Microvision v5.24.2
using a generic Cortex-M3 model as target device. For comparison, the currently
fastest implementation of Saturnin has a (simulated) encryption time of 5494
cycles and a decryption time of 5489 cycles on a generic Cortex-M3 device. 10
Consequently, Trax-L-17 outperforms Saturnin by a factor of more than 2.2.
The use of 32-bit operations implies that it is possible to vectorize the com- putation of several parallel Trax-L-17 instances on many platforms, meaning that its speed can be multiplied whenever e.g. AVX instructions are available.