Sparkle Suite

A collection of lightweight symmetric cryptographic primitives, finalist of the ongoing NIST lightweight standardisation effort.

Sparkle, a lightweight cryptographic permutation

Sparkle is a family of cryptographic permutations, each operating on a different block size (256, 384 or 512 bits). They rely only on Addition, Rotations and XORs (ARX paradigm). It is possible to write a unique implementation for all variants that simply takes the block size and the number of steps as inputs. It relies on the 64-bit transformation called Alzette. We denote it \(A_c\). The following constants are used to instantiate Alzette in Sparkle:

\[c_0 = \mathtt{b7e15162}, c_1 = \mathtt{bf715880}, c_2 = \mathtt{38b4da56}, c_3 = \mathtt{324e7738},\] \[c_4 = \mathtt{bb1185eb}, c_5 = \mathtt{4f7c7b57}, c_6 = \mathtt{cfbfa1c8}, c_7 = \mathtt{c2b3293d}.\]

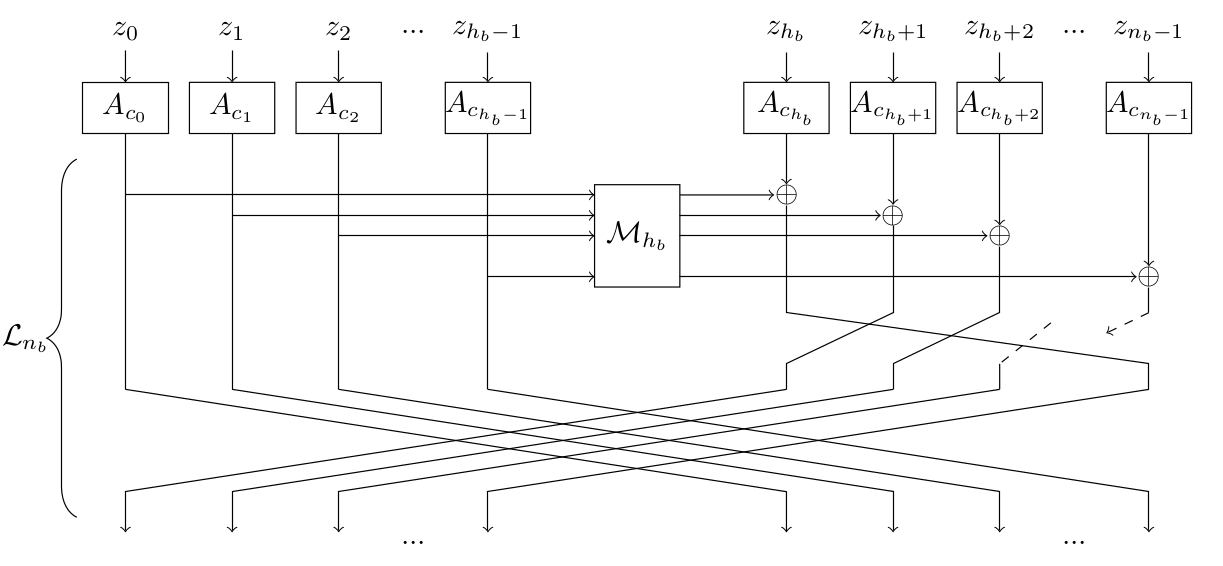
The picture below represents the round function of a Sparkle instance operating on \(64×n_b\) bits (note \(h_n = n_n / 2\)).

A diagram of the round function of `Sparkle`

The following code is a universal reference implementation of the Sparkle permutation in the C language. It accepts the input state, the total number \(n_b\) of branches, and the number \(n_s\) of steps. In particular, the following parameters are recommended:

  • for Sparkle256: \(n_b=4\), \(n_s = 10\) (full version) and \(n_s = 7\) (slim version);
  • for Sparkle384: \(n_b=6\), \(n_s = 11\) (full version) and \(n_s = 7\) (slim version);
  • for Sparkle512: \(n_b=8\), \(n_s = 12\) (full version) and \(n_s = 8\) (slim version).
#define MAX_BRANCHES 8
#define ROT(x, n) (((x) >> (n)) | ((x) << (32-(n))))
#define ELL(x) (ROT(((x) ^ ((x) << 16)), 16))
#define ALZETTE_ROUND(x, y, s, t, c) \
    (x) += ROT((y), (s));            \
    (y) ^= ROT((x), (t));            \
    (x) ^= (c);

// Round constants
static const uint32_t RCON[MAX_BRANCHES] = {      \
  0xB7E15162, 0xBF715880, 0x38B4DA56, 0x324E7738, \
  0xBB1185EB, 0x4F7C7B57, 0xCFBFA1C8, 0xC2B3293D  \
};

void sparkle(uint32_t *state, int nb, int ns)
{
  int i, j;  // Step and branch counter
  uint32_t rc, tmpx, tmpy, x0, y0;
  
  for(i = 0; i < ns; i ++) {
    // Counter addition
    state[1] ^= RCON[i%MAX_BRANCHES]; state[3] ^= i;
    // ARXBox layer
    for(j = 0; j < 2*nb; j += 2) {
      rc = RCON[j>>1];
      ALZETTE_ROUND(state[j], state[j+1], 31, 24, rc);
      ALZETTE_ROUND(state[j], state[j+1], 17, 17, rc);
      ALZETTE_ROUND(state[j], state[j+1],  0, 31, rc);
      ALZETTE_ROUND(state[j], state[j+1], 24, 16, rc);
    }
    // Linear layer
    tmpx = x0 = state[0];
    tmpy = y0 = state[1];
    for(j = 2; j < nb; j += 2) {
      tmpx ^= state[j]; tmpy ^= state[j+1];
    }
    tmpx = ELL(tmpx); tmpy = ELL(tmpy);
    for (j = 2; j < nb; j += 2) {
      state[j-2] = state[j+nb] ^ state[j] ^ tmpy;
      state[j+nb] = state[j];
      state[j-1] = state[j+nb+1] ^ state[j+1] ^ tmpx;
      state[j+nb+1] = state[j+1];
    }
    state[nb-2] = state[nb] ^ x0 ^ tmpy; state[nb] = x0;
    state[nb-1] = state[nb+1] ^ y0 ^ tmpx; state[nb+1] = y0;
  }
}